4. Случайная величина. Закон распределения
Определение случайной величины. Многие случайные события могут быть оценены количественно как случайные величины. Случайной называют такую величину, которая принимает значения в зависимости от стечения случайных обстоятельств. Различают дискретные и непрерывные случайные величины.
Распределение дискретной случайной величины. Дискретная величина считается заданной, если указаны возможные ее значения и соответствующие им вероятности. Обозначим дискретную случайную величину х, ее значения х1, х2..., в вероятности: Р (х1) =р2, Р (х2) = р2 и т. д.
Совокупность x и Р называется распределением дискретной случайной величины.
Так как все возможные значения дискретной случайной величины представляют полную систему, то сумма вероятностей равна единице:
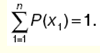
Здесь предполагается, что дискретная случайная величина имеет n значений. Выражение называется условием нормировки.
Во многих случаях наряду с распределением случайной величины или вместо него информацию об этих величинах могут дать числовые параметры, получившие название числовых характеристик случайной величины. Наиболее употребительные из них:
1) математическое ожидание (среднее значение) случайной величины есть сумма произведений всех возможных ее значений на вероятности этих значений;
2) дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
Для непрерывной случайной величины математическое ожидание и дисперсия записываются в виде:
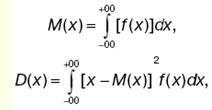
где f(x) - плотность вероятности или функция распределения вероятностей. Она показывает, как изменяется вероятность отнесения к интервалу dx случайной величины в зависимости от значения самой этой величины. Нормальный закон распределения. В теориях вероятностей и математической статистики, в различных приложениях важную роль играет нормальный закон распределения (закон Гаусса). Случайная величина распределена по этому закону, если плотность ее вероятности имеет вид:
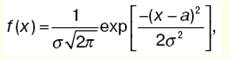
где а = М(х) - математическое ожидание случайной величины;
σ - среднее квадратное отклонение; следовательно;
σ2- дисперсия случайной величины. Кривая нормального закона распределения имеет колоколообразную форму, симметричную относительно прямой x = а (центр рассеивания).
Автор: Подколзина В.А.
<< Назад: Медицинская метрология и ее специфика
>> Вперед: Распределение Максвелла (распределение газовых молекул по скоростям) и Больцмана
 Рекомендуем интересные статьи раздела Конспекты лекций, шпаргалки:
Рекомендуем интересные статьи раздела Конспекты лекций, шпаргалки:
▪ Нервные болезни. Шпаргалка
▪ Страхование. Конспект лекций
▪ Госпитальная педиатрия. Шпаргалка
 Смотрите другие статьи раздела Конспекты лекций, шпаргалки.
Смотрите другие статьи раздела Конспекты лекций, шпаргалки.
 Читайте и пишите полезные комментарии к этой статье.
Читайте и пишите полезные комментарии к этой статье.
<< Назад
 Последние новости науки и техники, новинки электроники:
Последние новости науки и техники, новинки электроники:
Лабораторная модель прогнозирования землетрясений
30.11.2025
Предсказание землетрясений остается одной из самых сложных задач геофизики. Несмотря на развитие сейсмологии, ученые все еще не могут точно определить момент начала разрушительного движения разломов. Недавние эксперименты американских исследователей открывают новые горизонты: впервые удалось наблюдать микроскопические изменения в контактной зоне разломов, которые предшествуют землетрясению.
Группа под руководством Сильвена Барбота обнаружила, что "реальная площадь контакта" - участки, где поверхности разлома действительно соприкасаются - изменяется за миллисекунды до высвобождения накопленной энергии. "Мы открыли окно в сердце механики землетрясений", - отмечает Барбот. Эти изменения позволяют фиксировать этапы зарождения сейсмического события еще до появления традиционных сейсмических волн.
Для наблюдений ученые использовали прозрачные акриловые материалы, через которые можно было отслеживать световые изменения в зоне контакта. В ходе искусственного моделирования примерно 30% ко ...>>
Музыка как естественный анальгетик
30.11.2025
Ученые все активнее исследуют немедикаментозные способы облегчения боли. Одним из перспективных направлений становится использование музыки, которая способна воздействовать на эмоциональное состояние и когнитивное восприятие боли. Новое исследование международной группы специалистов демонстрирует, что даже кратковременное прослушивание любимых композиций может значительно снижать болевые ощущения у пациентов с острой болью в спине.
В эксперименте участвовали пациенты, обратившиеся за помощью в отделение неотложной помощи с выраженной болью в спине. Им предлагалось на протяжении десяти минут слушать свои любимые музыкальные треки. Уже после этой короткой сессии врачи фиксировали заметное уменьшение интенсивности боли как в состоянии покоя, так и при движениях.
Авторы исследования подчеркивают, что музыка не устраняет саму причину боли. Тем не менее, она воздействует на эмоциональный фон пациента, снижает уровень тревожности и отвлекает внимание, что в сумме приводит к субъективном ...>>
Алкоголь может привести к слобоумию
29.11.2025
Проблема влияния алкоголя на стареющий мозг давно вызывает интерес как у врачей, так и у исследователей когнитивного старения. В последние годы стало очевидно, что границы "безопасного" употребления спиртного размываются, и новое крупное исследование, проведенное международной группой ученых, вновь указывает на это. Работы Оксфордского университета, выполненные совместно с исследователями из Йельского и Кембриджского университетов, показывают: даже небольшие дозы алкоголя способны ускорять когнитивный спад.
Команда проанализировала данные более чем 500 тысяч участников из британского биобанка и американской Программы миллионов ветеранов. Дополнительно был выполнен метаанализ сорока пяти исследований, в общей сложности включавших сведения о 2,4 миллиона человек. Такой масштаб позволил оценить не только прямую связь между употреблением спиртного и развитием деменции, но и влияние генетической предрасположенности.
Один из наиболее тревожных результатов касается людей с повышенным ге ...>>
 Случайная новость из Архива Случайная новость из Архива Ищейки ртути
07.06.2000
В Швеции обучают полицейских собак вынюхивать ртуть. Несколько лет назад шведский парламент решил, что все старые, ненужные запасы ртути и отходы, содержащие этот опасный металл, должны быть обезврежены к 2001 году.
Много ртути в старых манометрах, барометрах, градусниках, но их сравнительно легко найти. Труднее обнаруживать ртуть в коленчатых сифонах под раковинами рукомойников в кабинетах стоматологов (амальгамы ртути применяются для изготовления зубных пломб), а также под полом в химических и других лабораториях, где она могла накапливаться годами из мелких, случайно падающих капелек. Ее находят собаки, реагирующие на запах даже одного миллиграмма ртути. В день каждая овчарка проверяет до 110 сифонов.
За два года две тренированные овчарки нашли 10 тонн ртути, из них 1,3 тонны в школах, где ртуть еще сравнительно недавно применялась в демонстрационных опытах, а то и в лабораторных работах учащихся. Предполагается, что осталось найти еще около 40 тонн, в основном на промышленных предприятиях. Кроме того, надо решить, где можно устроить надежные и безопасные захоронения ртути.
Подобную программу по поиску ртути с помощью собак собирается предпринять Норвегия.
|
 Другие интересные новости:
Другие интересные новости:
▪ Диск нашей галактики искривлен по краям
▪ Защищенный планшет Dell Latitude 7212 Rugged Extreme Tablet
▪ Сверхтонкая кнопка от Panasonic
▪ Зима - сезон вулканов
▪ Влияние сердца на чувства
 Лента новостей науки и техники, новинок электроники
Лента новостей науки и техники, новинок электроники
 Интересные материалы Бесплатной технической библиотеки:
Интересные материалы Бесплатной технической библиотеки:
▪ раздел сайта Защита электроаппаратуры. Подборка статей
▪ статья Тристан Бернар. Знаменитые афоризмы
▪ статья Почему болельщики венского Рапида последние 15 минут каждого матча непрерывно аплодируют? Подробный ответ
▪ статья Жиловщик мяса и субпродуктов. Должностная инструкция
▪ статья Измерение нелинейности напряжения развертки. Энциклопедия радиоэлектроники и электротехники
▪ статья Микропередатчик УКВ к телефону. Энциклопедия радиоэлектроники и электротехники
 Оставьте свой комментарий к этой статье:
Оставьте свой комментарий к этой статье:
Главная страница | Библиотека | Статьи | Карта сайта | Отзывы о сайте

www.diagram.com.ua
2000-2025






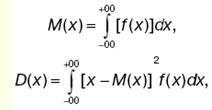
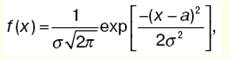
 Смотрите другие статьи раздела
Смотрите другие статьи раздела 