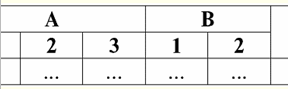
Лекция № 3. Реляционные объекты данных

1. Требования к табличной форме представления отношений

1. Самое первое требование, предъявляемое к табличной форме представления отношений, - это конечность. Работать с бесконечными таблицами, отношениями или любыми другими представлениями и организациями данных неудобно, редко оправдываются затраченные усилия, и, кроме того, подобное направление имеет малое практическое приложение.

Но помимо этого, вполне ожидаемого, существуют и другие требования.

2. Заголовок таблицы, представляющей отношение, должен обязательно состоять из одной строки - заголовка столбцов, причем с уникальными именами. Многоярусных заголовков не допускается. Например, таких:

Все многоярусные заголовки заменяются одноярусными путем подбора подходящих заголовков. В нашем примере таблица после указанных преобразований будет выглядеть следующим образом:

Мы видим, что имя каждого столбца уникально, поэтому их можно как угодно менять местами, т. е. их порядок становится несущественным.

А это очень важно, поскольку является третьим свойством.

3. Порядок строк должен быть несущественным. Однако это требование также не является строго ограничительным, так как можно без труда привести любую таблицу к требуемому виду. Например, можно ввести дополнительный столбец, который будет определять порядок строк. В этом случае от перестановки строк тоже ничего не изменится. Вот пример такой таблицы:

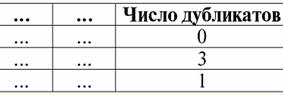
4. В таблице, представляющей отношение, не должно быть строк-дубликатов. Если же в таблице встречаются повторяющиеся строки, это можно легко исправить введением дополнительного столбца, отвечающего за количество дубликатов каждой строки, например:

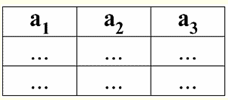
Следующее свойство также является вполне ожидаемым, потому что лежит в основе всех принципов программирования и проектирования реляционных баз данных.

5. Данные во всех столбцах должны быть одного и того же типа. И кроме того они должны быть простого типа.

Поясним, что такое простой и сложный типы данных.

Простой тип данных - это такой тип, значения данных которого не являются составными, т. е. не содержат составных частей. Таким образом, в столбцах таблицы не должны присутствовать ни списки, ни массивы, ни деревья, ни подобные названным составные объекты.

Такие объекты - составной тип данных - в реляционных системах управления базами данных сами представляются в виде самостоятельных таблиц-отношений.

2. Домены и атрибуты

Домены и атрибуты - базовые понятия в теории создания баз данных и управления ими. Поясним, что же это такое.

Формально, домен атрибута (обозначается dom(a)), где а - некий атрибут, определяется как множество допустимых значений одного и того же типа соответствующего атрибута а. Этот тип должен быть простым, т. е:

dom(a) ⊆ {x | type(x) = type(a)};

Атрибут (обозначается а), в свою очередь, определяется как упорядоченная пара, состоящая из имени атрибута name(a) и домена атрибута dom(a), т. е.:

a = (name(a): dom(a));

В этом определении вместо привычного знака "," (как в стандартных определениях упорядоченных пар) используется ":". Это делается для того, чтобы подчеркнуть ассоциацию домена атрибута и типа данных атрибута.

Приведем несколько примеров различных атрибутов:

а₁ = (Курс: {1, 2, 3, 4, 5});

а₂ = (МассаКг: {x | type(x) = real, x 0});

а₃ = (ДлинаСм: {x | type(x) = real, x 0});

Заметим, что у атрибутов а₂ и а₃ домены формально совпадают. Но семантическое значение этих атрибутов различно, ведь сравнивать значения массы и длины бессмысленно. Поэтому домен атрибута ассоциируется не только с типом допустимых значений, но и семантическим значением.

В табличной форме представления отношений атрибут отображается как заголовок столбца таблицы, и при этом домен атрибута не указывается, но подразумевается. Это выглядит следующим образом:

Нетрудно заметить, что здесь каждый из заголовков a₁, a₂, a₃ столбцов таблицы, представляющей какое-то отношение, является отдельным атрибутом.

3. Схемы отношений. Именованные значения кортежей

В теории и практике СУБД понятия схемы отношения и именованного значения кортежа на атрибуте являются базовыми. Приведем их.

Схема отношения (обозначается S) определяется как конечное множество атрибутов с уникальными именами, т. е.:

S = {a | a ∈ S};

В каждой таблице, представляющей отношение, все заголовки столбцов (все атрибуты) объединяются в схему этого отношения.

Количество атрибутов в схеме отношений определяет степень этого отношения и обозначается как мощность множества: |S|.

Схема отношений может ассоциироваться с именем схемы отношений.

В табличной форме представления отношений, как нетрудно заметить, схема отношения - это не что иное, как строка заголовков столбцов.

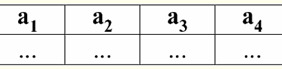
S = {a₁, a₂, a₃, a₄} - схема отношений этой таблицы.

Имя отношения изображается как схематический заголовок таблицы.

В текстовой же форме представления схема отношений может быть представлена как именованный список имен атрибутов, например:

Студенты (№ зачетной книжки, Фамилия, Имя, Отчество, Дата рождения).

Здесь, как и в табличной форме представления, домены атрибутов не указываются, но подразумеваются.

Из определения следует, что схема отношения может быть и пустой (S = ∅). Правда, возможно это только в теории, так как на практике система управления базами данных никогда не допустит создания пустой схемы отношения.

Именованное значение кортежа на атрибуте (обозначается t(a))определяется по аналогии с атрибутом как упорядоченная пара, состоящая из имени атрибута и значения атрибута, т. е.:

t(a) = (name(a) : x), x ∈ dom(a);

Видим, что значение атрибута берется из домена атрибута.

В табличной форме представления отношения каждое именованное значение кортежа на атрибуте - это соответствующая ячейка таблицы:

Здесь t(a₁), t(a₂), t(a₃) - именованные значения кортежа t на атрибутах а₁, а₂, а₃.

Простейшие примеры именованных значений кортежей на атрибутах:

(Курс: 5), (Балл: 5);

Здесь соответственно Курс и Балл - имена двух атрибутов, а 5 - это одно из их значений, взятое из их доменов. Разумеется, хоть эти значения в обоих случаях равны друг другу, семантически они различны, так как множества этих значений в обоих случаях отличаются друг от друга.

4. Кортежи. Типы кортежей

Понятие кортежа в системах управления базами данных может быть интуитивно найдено уже из предыдущего пункта, когда мы говорили об именованном значении кортежа на различных атрибутах. Итак, кортеж (обозначается t, от англ. tuple - "кортеж") со схемой отношения S определяется как множество именованных значений этого кортежа на всех атрибутах, входящих в данную схему отношений S. Другими словами, атрибуты берутся из области определения кортежа, def(t), т. е.:

t ≡ t(S) = {t(a) | a ∈ def(t) ⊆ S;.

Важно, что одному имени атрибута обязательно должно соответствовать не более одного значения атрибута.

В табличной форме записи отношения кортежем будет любая строка таблицы, т. е.:

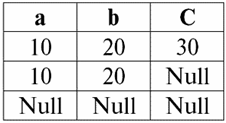
Здесь t₁(S) = {t(a₁), t(a₂), t(a₃), t(a₄)} и t₂(S) = {t(a₅), t(a₆), t(a₇), t(a₈)} - кортежи.

Кортежи в СУБД различаются по типам в зависимости от своей области определения. Кортежи называются:

1) частичными, если их область определения включается или совпадает со схемой отношения, т. е. def(t) ⊆ S.

Это общий случай в практике баз данных;

2) полными, в том случае если их область определения полностью совпадает, равна схеме отношения, т. е. def(t) = S;

3) неполными, если область определения полностью включается в схему отношений, т. е. def(t) ⊂ S;

4) нигде не определенными, если их область определения равна пустому множеству, т. е. def(t) = ∅.

Поясним на примере. Пусть у нас имеется отношение, заданное следующей таблицей.

Пусть здесь t₁ = {10, 20, 30}, t₂ = {10, 20, Null}, t₃ = {Null, Null, Null}. Тогда легко заметить, что кортеж t₁ - полный, так как его область определения def(t₁) = { a, b, c} = S.

Кортеж t₂ - неполный, def(t₂) = { a, b} ⊂ S. И, наконец, кортеж t₃ - нигде не определенный, так как его def(t3) = ∅.

Надо заметить, что нигде не определенный кортеж - это пустое множество, тем не менее ассоциируемое со схемой отношений. Иногда нигде не определенный кортеж обозначается: ∅(S). Как мы уже видели в приведенном примере, такой кортеж представляет собой строку таблицы, состоящую только из Null-значений.

Интересно, что сравнимыми, т. е. возможно равными, являются только кортежи с одной и той же схемой отношений. Поэтому, например, два нигде не определенных кортежа с различными схемами отношений не будут равными, как могло ожидаться. Они будут различными так же, как их схемы отношений.

5. Отношения. Типы отношений

И наконец дадим определение отношению, как некой вершине пирамиды, состоящей из всех предыдущих понятий. Итак, отношение (обозначается r, от англ. relation - "отношение") со схемой отношений S определяется как обязательно конечное множество кортежей, имеющих ту же схему отношения S. Таким образом:

r ≡ r(S) = {t(S) | t ∈r};

По аналогии со схемами отношений количество кортежей в отношении называют мощностью отношений и обозначают как мощность множества: |r|.

Отношения, как и кортежи, различаются по типам. Итак, отношения называются:

1) частичными, если для любого входящего в отношение кортежа выполняется следующее условие: [def(t) ⊆ S].

Это (как и с кортежами) общий случай;

2) полными, в том случае если ∀t ∈ r(S) выполняется: [def(t) = S];

3) неполными, если ∃t ∈ r(S) def(t) ⊂ S;

4) нигде не определенными, если ∀t ∈ r(S) [def(t) = ∅].

Обратим отдельное внимание на нигде не определенные отношения. В отличие от кортежей работа с такими отношениями включает в себя небольшую тонкость. Дело в том, что нигде не определенные отношения могут быть двух видов: они могут быть либо пустыми, либо могут содержать единственный нигде не определенный кортеж (такие отношения обозначаются {∅(S)}).

Сравнимыми (по аналогии с кортежами), т. е., возможно равными, являются лишь отношения с одной и той же схемой отношения. Поэтому отношения с различными схемами отношений являются различными.

В табличной форме представления, отношение - это тело таблицы, которому соответствует строка - заголовок столбцов, т. е. буквально - вся таблица, вместе с первой строкой, содержащей заголовки.

<< Назад: Отсутствующие данные (Пустые значения (Empty-значения). Неопределенные значения (Null-значения). Null-значения и общее правило вычисления выражений. Null-значения и логические операции. Null-значения и проверка условий)

>> Вперед: Реляционная алгебра. Унарные операции (Унарная операция выборки. Унарная операция проекции. Унарная операция переименования. Свойства унарных операций)

Рекомендуем интересные статьи раздела Конспекты лекций, шпаргалки:

▪ Медицинская статистика. Шпаргалка

▪ Теория обучения. Конспект лекций

▪ Управление персоналом. Шпаргалка

Смотрите другие статьи раздела Конспекты лекций, шпаргалки.

Читайте и пишите полезные комментарии к этой статье.

<< Назад

Последние новости науки и техники, новинки электроники:

Экраны влияют на детей неравномерно в разном возрасте 01.08.2026

Планшеты и смартфоны давно стали привычной частью повседневной жизни даже самых маленьких детей. Родители часто используют гаджеты, чтобы успокоить малыша или занять его на время, однако ученые все чаще задаются вопросом, как экранное время сказывается на развитии мозга и будущей способности к обучению. Новое исследование показывает, что значение имеет не только продолжительность просмотра, но и возраст, в котором ребенок проводит время перед экраном. Ученые наблюдали детей от рождения до 8 лет. Оказалось, что больше всего экраны влияют на мозг в два периода - в раннем младенческом возрасте и перед поступлением в школу. У детей, много времени проводивших перед экранами в эти возрастные точки, в 9 лет были несколько хуже успехи в обучении, а в 10,5 лет хуже работала рабочая память - способность удерживать и обрабатывать информацию здесь и сейчас. Исследователи из Франции и Сингапура проанализировали данные 502 детей и выделили два ключевых этапа. У младенцев мозг развивается очень ...>>

Умные жилеты, спасающие от жары 01.08.2026

Летняя жара в больших городах все чаще становится серьезным испытанием для людей, работающих на открытом воздухе. Мусорщики, строители и другие специалисты вынуждены проводить часы под палящим солнцем, рискуя перегревом. Китайские инженеры предложили практичное решение - специальные охлаждающие жилеты, которые помогают снизить ощущаемую температуру примерно на 10 градусов. Пока мир страдает от сильной жары, китайские инженеры разработали "умные" жилеты с климат-контролем. Жилеты с кондиционированием почти не отличаются от обычной рабочей одежды. Главное отличие - в системе охлаждения. В городе Нанкин в жилет вмонтированы два вентилятора, работающих от портативных аккумуляторов. Одного заряда хватает на 3-4 часа непрерывной работы. В Чанчжоу решили разместить в карманах охлаждающие элементы с материалом, который при нагревании переходит из твердого состояния в жидкое, активно поглощая тепло. Это поддерживает комфортную температуру в течение 2,5-4 часов. Такие жилеты выглядят почти ...>>

Летающие ветротурбины 3 МВт вышли в серию 31.07.2026

Традиционные ветряные электростанции зависят от силы и стабильности ветра у поверхности земли, где воздушные потоки часто бывают слабыми и порывистыми. На больших высотах ветер обычно сильнее и постояннее, поэтому инженеры уже давно рассматривают возможность подъема турбин в воздух. Китайская компания сделала важный шаг в этом направлении, перейдя от испытаний к мелкосерийному производству. Компания Beijing Linyi Yunchuan Energy Technology запустила мелкосерийное производство летающей ветротурбины S2000, а в провинции Чжэцзян возводят отдельный завод по производству материалов для оболочки аппарата. У компании уже есть предварительные договоренности с прибрежными городами и горными регионами, которые рассматривают возможность использования этой технологии для удовлетворения собственных энергетических потребностей. Прототип, который полгода назад только что поднялся в небо над Сычуанем, теперь превращается в целую отрасль. Идея S2000 проста: вместо того чтобы устанавливать ветряну ...>>

Случайная новость из Архива Самогон вместо бензина 11.05.2009 Американская компания "Е-Fuel" вышла на рынок с самогонным аппаратом, рассчитанным на производство этилового спирта из сахара, чтобы заменить спиртом бензин в автомобиле. Покупателям предлагается устройство размером с большой холодильник, которое вырабатывает за неделю до 132 литров спирта, причем это горючее будет обходиться в два-три раза дешевле бензина. Кроме сахара как сырье годятся отходы винокурения, пивоварения и переработки фруктов. Фирма надеется продать до 200 тысяч таких установок. Критики идеи указывают, что сахар слишком дорог, а двигатель автомобиля придется существенно переделывать под чистый спирт. Однако производитель утверждает, что дешевый сахар можно беспошлинно импортировать из Мексики, где наблюдается его перепроизводство, а отходы виноделов и пивоваров вообще бесплатные.

Другие интересные новости:

▪ Мобильный телефон, работающий без сотовых операторов

▪ Жидкокристаллический кабель для передачи тока

▪ Проект Proba-3 - искусственное солнечное затмение

▪ Двойной объектив для съемки VR-контента от Canon

▪ Высокоточный оптический зонд для изучения человеческого мозга

Лента новостей науки и техники, новинок электроники

Интересные материалы Бесплатной технической библиотеки:

▪ раздел сайта Крылатые слова, фразеологизмы. Подборка статей

▪ статья Георг Зиммель. Знаменитые афоризмы

▪ статья Почему жителей города Торжок называют новоторами? Подробный ответ

▪ статья Оператор на автоматических и полуавтоматических линиях, занятый операциями сверления и присадки. Типовая инструкция по охране труда

▪ статья Малогабаритный регулятор мощности. Энциклопедия радиоэлектроники и электротехники

▪ статья Грязь сквозь руку. Секрет фокуса

Оставьте свой комментарий к этой статье:

www.diagram.com.ua
2000-2026