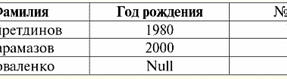
Лекция № 2. Отсутствующие данные

В системах управления базами данных для определения отсутствующих данных описаны два вида значений: пустые (или Empty-значения) и неопределенные (или Null-значения).

В некоторой (преимущественно коммерческой) литературе на Null-значения иногда ссылаются как на пустые или нулевые значения, однако это неверно. Смысл пустого и неопределенного значения принципиально различается, поэтому необходимо внимательно следить за контекстом употребления того или иного термина.

1. Пустые значения (Empty-значения)

Пустое значение - это просто одно из множества возможных значений какого-то вполне определенного типа данных.

Перечислим наиболее "естественные", непосредственные пустые значения (т. е. пустые значения, которые мы могли бы выделить самостоятельно, не имея никакой дополнительной информации):

1) 0 (нуль) - нулевое значение является пустым для числовых типов данных;

2) false (неверно) - является пустым значением для логического типа данных;

3) B’’ - пустая строка бит для строк переменной длины;

4) "" - пустая строка для строк символов переменной длины.

В приведенных выше случаях определить, пустое значение или нет, можно путем сравнивания имеющегося значения с константой пустого значения, определенной для каждого типа данных. Но системы управления базами данных в силу реализованных в них схем долговременного хранения данных могут работать только со строками постоянной длины. Из-за этого пустой строкой бит можно назвать строку двоичных нулей. Или строку, состоящую из пробелов или каких-либо других управляющих символов, - пустой строкой символов.

Вот несколько примеров пустых строк постоянной длины:

1) B’0’;

2) B’000’;

3) ‘ ‘.

Как же в этих случаях определить, является ли строка пустой?

В системах управления базами данных для проверки на пустоту применяется логическая функция, т. е. предикат IsEmpty (<выражение>), что буквально означает "есть пустой". Этот предикат обычно встроен в систему управления базами данных и может применяться к выражению абсолютно любого типа. Если такого предиката в системах управления базами данных нет, то можно написать логическую функцию самим и включить ее в список объектов проектируемой базы данных.

Рассмотрим еще один пример, когда не так просто определить, пустое ли мы имеем значение. Данные типа "дата". Какое значение в этом типе считать пустым значением, если дата может варьироваться в диапазоне от 01.01.0100. до 31.12.9999? Для этого в СУБД вводится специальное обозначение для константы пустой даты {...}, если значения этого типа записывается: {ДД. ММ. ГГ} или {ГГ. ММ. ДД}. С этим значением и происходит сравнение при проверке значения на пустоту. Оно считается вполне определенным, "полноправным" значением выражения этого типа, причем наименьшим из возможных.

При работе с базами данных пустые значения часто используются как значения по умолчанию или применяются, если значения выражений отсутствуют.

2. Неопределенные значения (Null-значения)

Слово Null используется для обозначения неопределенных значений в базах данных.

Чтобы лучше понять, какие значения понимаются под неопределенными, рассмотрим таблицу, являющуюся фрагментом базы данных:

Итак, неопределенное значение или Null-значение - это:

1) неизвестное, но обычное, т. е. применимое значение. Например, у господина Хайретдинова, который является номером один в нашей базе данных, несомненно, имеются какие-то паспортные данные (как у человека 1980 г. рождения и гражданина страны), но они не известны, следовательно, не занесены в базу данных. Поэтому в соответствующую графу таблицы будет записано значение Null;

2) неприменимое значение. У господина Карамазова (№ 2 в нашей базе данных) просто не может быть никаких паспортных данных, потому что на момент создания этой базы данных или внесения в нее данных, он являлся ребенком;

3) значение любой ячейки таблицы, если мы не можем сказать применимое оно или нет. Например, у господина Коваленко, который занимает третью позицию в составленной нами базе данных, неизвестен год рождения, поэтому мы не можем с уверенностью говорить о наличие или отсутствии у него паспортных данных. А следовательно, значениями двух ячеек в строке, посвященной господину Коваленко будет Null-значение (первое - как неизвестное вообще, второе - как значение, природа которого неизвестна). Как и любые другие типы данных, Null-значения тоже имеют определенные свойства. Перечислим самые существенные из них:

1) с течением времени понимание Null-значения может меняться. Например, у господина Карамазова (№ 2 в нашей базе данных) в 2014 г., т. е. по достижении совершеннолетия, Null-значение изменится на какое-то конкретное вполне определенное значение;

2) Null-значение может быть присвоено переменной или константе любого типа (числового, строкового, логического, дате, времени и т. д.);

3) результатом любых операций над выражениями с Null-значе-ниями в качестве операндов является Null-значение;

4) исключением из предыдущего правила являются операции конъюнкции и дизъюнкции в условиях законов поглощения (подробнее о законах поглощения смотрите в п. 4 лекции № 2).

3. Null-значения и общее правило вычисления выражений

Поговорим подробнее о действиях над выражениями, содержащими Null-значения.

Общее правило работы с Null-значениями (то, что результат операций над Null-значениями есть Null-значение) применяется к следующим операциям:

1) к арифметическим;

2) к побитным операциям отрицания, конъюнкции и дизъюнкции (кроме законов поглощения);

3) к операциям со строками (например, конкотинации - сцепления строк);

4) к операциям сравнения (<, ≤, ≠, ≥, >).

Приведем примеры. В результате применений следующих операций будут получены Null-значения:

3 + Null, 1/ Null, (Иванов' + '' + Null) ≔ Null

Здесь вместо обычного равенства использована операция подстановки "≔" из-за особого характера работы с Null-значениями. Далее в подобных ситуациях также будет использоваться этот символ, который означает, что выражение справа от символа подстановки может заменить собой любое выражение из списка слева от символа подстановки.

Характер Null-значений приводит к тому, что часто в некоторых выражениях вместо ожидаемого нуля получается Null-значение, например:

(x - x), y * (x - x), x * 0 ≔ Null при x = Null.

Все дело в том, что при подстановке, например, в выражение (x - x) значения x = Null, мы получаем выражение (Null - Null), и в силу вступает общее правило вычисления значения выражения, содержащего Null-значения, и информация о том, что здесь Null-значение соответствует одной и той же переменной теряется.

Можно сделать вывод, что при вычислении любых операций, кроме логических, Null-значения интерпретируются как неприменимые, и поэтому в результате получается тоже Null-значение.

К не менее неожиданным результатам приводит использование Null-значений в операциях сравнения. Например, в следующих выражениях также получаются Null-значения вместо ожидаемых логических значений True или False:

(Null < Null); (Null ≤ Null); (Null = Null); (Null ≠ Null);

(Null > Null); (Null ≥ Null) ≔ Null;

Таким образом, делаем вывод, что нельзя говорить о том, что Null-значение равно или не равно самому себе. Каждое новое вхождение Null-значения рассматривается как независимое, и каждый раз Null-значения воспринимаются как различные неизвестные значения. Этим Null-значения кардинально отличаются от всех остальных типов данных, ведь мы знаем, что обо всех пройденных ранее величинах и их типах с уверенностью можно было говорить, что они равны или не равны друг другу.

Итак, мы видим, что Null-значения не являются значениями переменных в обычном смысле этого слова. Поэтому становится невозможным сравнивать значения переменных или выражения, содержащие Null-значения, поскольку в результате мы будем получать не логические значения True или False, а Null-значения, как в следующих примерах:

(x < Null); (x ≤ Null); (x = Null); (x ≠ Null); (x > Null);

(x ≥ Null) ≔ Null;

Поэтому по аналогии с пустыми значениями для проверки выражения на Null-значения необходимо использовать специальный предикат:

IsNull (<выражение>), что буквально означает "есть Null".

Логическая функция возвращает значение True, если в выражении присутствует Null или оно равно Null, и False - в противном случае, но никогда не возвращает значение Null. Предикат IsNull может применяться к переменным и выражению любого типа. Если применять его к выражениям пустого типа, предикат всегда будет возвращать False.

Например:

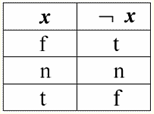
Итак, действительно, видим, что в первом случае, когда предикат IsNull взяли от нуля, на выходе получилось значение False. Во всех случаях, в том числе во втором и третьем, когда аргументы логической функции оказались равными Null-значению, и в четвертом случае, когда сам аргумент и был изначально равен Null-значению, предикат выдал значение True.

4. Null-значения и логические операции

Обычно в системах управления базами данных непосредственно поддерживаются только три логические операции: отрицание ¬, конъюнкция & и дизъюнкция ∨. Операции следования ⇒ и равносильности ⇔ выражаются через них с помощью подстановок:

(x ⇒ y) ≔ (¬x ∨ y);

(x ⇔ y) ≔ (x ⇒ y) & (y ⇒ x);

Заметим, что эти подстановки полностью сохраняются и при использовании Null-значений.

Интересно, что при помощи операции отрицания "¬" любая из операций конъюнкция & или дизъюнкция ∨ может быть выражена одна через другую следующим образом:

(x & y) ≔¬ (¬x ∨¬y);

(x ∨ y) ≔ ¬ (¬x & ¬y);

На эти подстановки, как и на предыдущие, Null-значения влияния не оказывают.

А теперь приведем таблицы истинности логических операций отрицания, конъюнкции и дизъюнкции, но кроме привычных значений True и False, используем также Null-значение в качестве операндов. Для удобства введем следующие обозначения: вместо True будем писать t, вместо False - f, а вместо Null - n.

1. Отрицание ¬x.

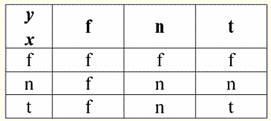
Стоит отметить следующие интересные моменты касательно операции отрицания с использованием Null-значений:

1) ¬¬x ≔ x - закон двойного отрицания;

2) ¬Null ≔ Null - Null-значение является неподвижной точкой.

2. Конъюнкция x & y.

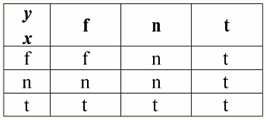
Эта операция также имеет свои свойства:

1) x & y ≔ y & x- коммутативность;

2) x & x ≔ x - идемпотентность;

3) False & y ≔ False, здесь False - поглощающий элемент;

4) True & y ≔ y, здесь True - нейтральный элемент.

3. Дизъюнкция x ∨ y.

Свойства:

1) x ∨ y ≔ y ∨ x - коммутативность;

2) x ∨ x ≔ x - идемпотентность;

3) False ∨ y ≔ y, здесь False - нейтральный элемент;

4) True ∨ y ≔ True, здесь True - поглощающий элемент.

Исключение из общего правила составляют правила вычисления логических операций конъюнкция & и дизъюнкция ∨ в условиях действия законов поглощения:

(False & y) ≔ (x & False) ≔ False;

(True ∨ y) ≔ (x ∨ True) ≔ True;

Эти дополнительные правила формулируются для того, чтобы при замене Null-значения значениями False или True результат бы все равно не зависел бы от этого значения.

Как и ранее было показано для других типов операций, применение Null-значений в логических операциях могут также привести к неожиданным значениям. Например, логика на первый взгляд нарушена в законе исключения третьего (x ∨ ¬x) и в законе рефлексивности (x = x), поскольку при x ≔ Null имеем:

(x ∨ ¬x), (x = x) ≔ Null.

Законы не выполняются! Объясняется это так же, как и раньше: при подстановке Null-значения в выражение информация о том, что это значение сообщается одной и той же переменной теряется, а в силу вступает общее правило работы с Null-значениями.

Таким образом, делаем вывод: при выполнении логических операций с Null-значениями в качестве операнда эти значения определяются системами управления базами данных как применимое, но неизвестное.

5. Null-значения и проверка условий

Итак, из всего вышесказанного можно сделать вывод, что в логике систем управления базами данных имеются не два логических значения (True и False), а три, ведь Null-значение также рассматривается как одно из возможных логических значений. Именно поэтому на него часто ссылаются как на неизвестное значение, значение Unknown.

Однако, несмотря на это, в системах управления базами данных реализуется только двузначная логика. Поэтому условие с Null-значением (неопределенное условие) должно интерпретироваться машиной либо как True, либо как False.

В языке СУБД по умолчанию установлено опознавание условия с Null-значением как значения False. Проиллюстрируем это следующими примерами реализации в системах управления базами данных условных операторов If и While:

If P then A else B;

Эта запись означает: если P принимает значение True, то выполняется действие A, а если P принимает значение False или Null, то выполняется действие B.

Теперь применим к этому оператору операцию отрицания, получим:

If ¬P then B else A;

В свою очередь, этот оператор означает следующее: если ¬P принимает значение True, то выполняется действие B, а в том случае, если ¬P принимает значение False или Null, то будет выполняться действие A.

И снова, как мы видим, при появлении Null-значения мы сталкиваемся с неожиданными результатами. Дело в том, что два оператора If в этом примере не эквивалентны! Хотя один из них получен из другого отрицанием условия и перестановкой ветвей, т. е. стандартной операцией. Такие операторы в общем случае эквивалентны! Но в нашем примере мы видим, что Null-значению условия P в первом случае соответствует команда B, а во втором - A.

А теперь рассмотрим действие условного оператора While:

While P do A; B;

Как работает этот оператор? Пока переменная P имеет значение True, будет выполняться действие A, а как только P примет значение False или Null, выполнится действие B.

Но не всегда Null-значения интерпретируются как False. Например, в ограничениях целостности неопределенные условия опознаются как True (ограничения целостности - это условия, накладываемые на входные данные и обеспечивающие их корректность). Это происходит потому, что в таких ограничениях отвергнуть нужно только заведомо ложные данные.

И опять-таки в системах управления базами данных существует специальная функция подмены IfNull (ограничения целостности, True), с помощью которой Null-значения и неопределенные условия можно представить в явном виде.

Перепишем условные операторы If и While с использованием этой функции:

1) If IfNull ( P, False) then A else B;

2) While IfNull ( P, False) do A; B;

Итак, функция подмены IfNull (выражение 1, выражение 2) возвращает значение первого выражения, если оно не содержит Null-значения, и значение второго выражения - в противном случае.

Надо заметить, что на тип возвращаемого функцией IfNull выражения никаких ограничений не накладывается. Поэтому с помощью этой функции можно явно переопределить любые правила работы с Null-значениями.

<< Назад: Введение (Системы управления базами данных. Реляционные базы данных)

>> Вперед: Реляционные объекты данных (Требования к табличной форме представления отношений. Домены и атрибуты. Схемы отношений. Именованные значения кортежей. Кортежи. Типы кортежей. Отношения. Типы отношений)

Рекомендуем интересные статьи раздела Конспекты лекций, шпаргалки:

▪ Криминология. Шпаргалка

▪ Педагогика. Шпаргалка

▪ История культуры. Конспект лекций

Смотрите другие статьи раздела Конспекты лекций, шпаргалки.

Читайте и пишите полезные комментарии к этой статье.

<< Назад

Последние новости науки и техники, новинки электроники:

Искусственная кожа для эмуляции прикосновений 15.04.2024

В мире современных технологий, где удаленность становится все более обыденной, сохранение связи и чувства близости играют важную роль. Недавние разработки немецких ученых из Саарского университета в области искусственной кожи представляют новую эру в виртуальных взаимодействиях. Немецкие исследователи из Саарского университета разработали ультратонкие пленки, которые могут передавать ощущение прикосновения на расстоянии. Эта передовая технология предоставляет новые возможности для виртуального общения, особенно для тех, кто оказался вдали от своих близких. Ультратонкие пленки, разработанные исследователями, толщиной всего 50 микрометров, могут быть интегрированы в текстильные изделия и носиться как вторая кожа. Эти пленки действуют как датчики, распознающие тактильные сигналы от мамы или папы, и как исполнительные механизмы, передающие эти движения ребенку. Прикосновения родителей к ткани активируют датчики, которые реагируют на давление и деформируют ультратонкую пленку. Эта ...>>

Кошачий унитаз Petgugu Global 15.04.2024

Забота о домашних животных часто может быть вызовом, особенно когда речь заходит о поддержании чистоты в доме. Представлено новое интересное решение стартапа Petgugu Global, которое облегчит жизнь владельцам кошек и поможет им держать свой дом в идеальной чистоте и порядке. Стартап Petgugu Global представил уникальный кошачий унитаз, способный автоматически смывать фекалии, обеспечивая чистоту и свежесть в вашем доме. Это инновационное устройство оснащено различными умными датчиками, которые следят за активностью вашего питомца в туалете и активируются для автоматической очистки после его использования. Устройство подключается к канализационной системе и обеспечивает эффективное удаление отходов без необходимости вмешательства со стороны владельца. Кроме того, унитаз имеет большой объем смываемого хранилища, что делает его идеальным для домашних, где живут несколько кошек. Кошачий унитаз Petgugu разработан для использования с водорастворимыми наполнителями и предлагает ряд доп ...>>

Привлекательность заботливых мужчин 14.04.2024

Стереотип о том, что женщины предпочитают "плохих парней", долгое время был широко распространен. Однако, недавние исследования, проведенные британскими учеными из Университета Монаша, предлагают новый взгляд на этот вопрос. Они рассмотрели, как женщины реагируют на эмоциональную ответственность и готовность помогать другим у мужчин. Результаты исследования могут изменить наше представление о том, что делает мужчин привлекательными в глазах женщин. Исследование, проведенное учеными из Университета Монаша, приводит к новым выводам о привлекательности мужчин для женщин. В рамках эксперимента женщинам показывали фотографии мужчин с краткими историями о их поведении в различных ситуациях, включая их реакцию на столкновение с бездомным человеком. Некоторые из мужчин игнорировали бездомного, в то время как другие оказывали ему помощь, например, покупая еду. Исследование показало, что мужчины, проявляющие сочувствие и доброту, оказались более привлекательными для женщин по сравнению с т ...>>

Случайная новость из Архива Телевизионная приставка Pipo X7 16.12.2014 Китайская компания Pipo представила телевизионную приставку X7, которая по ряду параметров выделяется из общей массы доступных на рынке устройств данного типа. Обычно ТВ-приставки используют связку из ARM-процессора того или иного производителя и операционной системы Android. Pipo при создании X7 сделала выбор в пользу платформы Wintel. Аппаратной основой новинки служит Intel Bay Trail, она комплектуется 22-нм 4-ядерным процессором Atom Z3735F или Atom Z3736F. В первом случае номинальная/форсированная частоты равны 1,33/1,83 ГГц, во втором - 1,33/2,16 ГГц. Обработкой графики занят встроенный контроллер Intel HD Graphics. В оснащение Pipo X7 входят 2 Гбайт оперативной памяти, флеш-накопитель (его объем не обнародован), слот MicroSD, Ethernet-контроллер, адаптеры беспроводной связи Wi-Fi 802.11b/g/n и Bluetooth, четыре порта USB и интерфейс HDMI. Размеры составляют 188 ? 129 ? 25,6 мм, вес - 440 г. На приставку установлена операционная система Windows 8.1 with Bing. Это означает, что пользователи смогут не только работать с веб-сервисами и мультимедийными материалами, но и запускать традиционные Windows-приложения.

Другие интересные новости:

▪ Беспроводная зарядка электромобилей на ходу

▪ Солдаты-киборги

▪ Новый магнитный материал для квантовых вычислений

▪ Экран с надувными зонами

▪ Китайский Питон ремонтирует дороги

Лента новостей науки и техники, новинок электроники

Интересные материалы Бесплатной технической библиотеки:

▪ раздел сайта Личный транспорт: наземный, водный, воздушный. Подборка статей

▪ статья После ужина горчица. Крылатое выражение

▪ статья Что мог делать автомат 1912 года, считающийся первой в мире компьютерной игрой? Подробный ответ

▪ статья Прораб. Должностная инструкция

▪ статья Цифровая система радиоуправления с частотным кодированием. Энциклопедия радиоэлектроники и электротехники

▪ статья Бусы исчезают и появляются вновь. Секрет фокуса

Оставьте свой комментарий к этой статье:

All languages of this page

Arabic	Hebrew	Polish
Bengali	Hindi	Portuguese
Chinese	Italian	Spanish
English	Japanese	Turkish
French	Korean	Ukrainian
German	Malay	Vietnamese

Главная страница | Библиотека | Статьи | Карта сайта | Отзывы о сайте

www.diagram.com.ua
2000-2024