|
Arabic
Bengali
Chinese
English
French
German
Hebrew
Hindi
Italian
Japanese
Korean
Malay
Polish
Portuguese
Spanish
Turkish
Ukrainian
Vietnamese
ЭНЦИКЛОПЕДИЯ РАДИОЭЛЕКТРОНИКИ И ЭЛЕКТРОТЕХНИКИ Расчет цепей переменного тока. Энциклопедия радиоэлектроники и электротехники
Энциклопедия радиоэлектроники и электротехники / Начинающему радиолюбителю Кроме резисторов, обладающих некоторым сопротивлением, в электрические цепи могут включаться катушки индуктивности и конденсаторы. Для постоянного тока их поведение просто и очевидно - катушка обладает некоторым сопротивлением, обычно небольшим, равным сопротивлению провода, которым она намотана, а конденсатор тока не проводит, и его сопротивление можно считать бесконечно большим (исключение - оксидные конденсаторы, имеющие небольшой ток утечки). Совершенно по-иному эти элементы ведут себя на переменном токе. В частности, на выводах катушки возникает ЭДС индукции, а ток через конденсатор начинает протекать, периодически перезаряжая пластины. Расскажем об этом подробнее. Переменный ток назван так потому, что он непрерывно изменяется во времени. Можно придумать множество всяких видов переменного тока, но обычно мы имеем дело с периодическим процессом, повторяющимся через определенный интервал времени, называемый периодом Т. Обратная ему величина называется частотой процесса: f = 1/Т. Это число колебаний или циклов за секунду. Немаловажное значение имеет и форма колебаний. Удобнее всего ее наблюдать с помощью осциллографа. Колебания могут быть периодической последовательностью импульсов, прямоугольными, треугольными и, вообще, какими угодно. Но оказывается, что любое, самое сложное периодическое колебание можно представить в виде суммы самых простых, синусоидальных колебаний с частотами f, 2f, 3f и т. д. Первое колебание с частотой f называют основной гармоникой, последующие - второй, третьей и т. д. гармониками. Математически это называется разложением в ряд Фурье, и таким способом чаще всего и анализируют прохождение сложных колебаний через различные радиотехнические цепи. Мы же пока займемся синусоидальными колебаниями, как основой любого, более сложного анализа. Синусоидальное (гармоническое) напряжение описывается функцией U = Umsin(ωt - φ0), график которой показан на рис. 11.
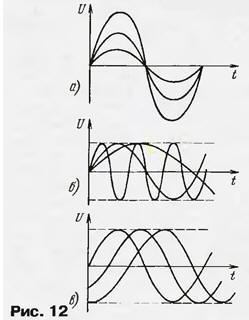
Аргументом функции является текущее время t, в зависимости от которого и изменяется напряжение U. Остальные величины служат параметрами колебания: Um - амплитудное значение напряжения, или просто амплитуда; ω = 2πf - угловая частота; φ0 - начальная фаза. Чтобы лучше понять значения этих параметров, на рис. 12, а, б, в показано, как влияют на колебания изменения амплитуды, частоты и начальной фазы.
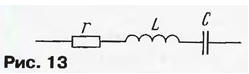
Когда говорят о переменном напряжении или токе, чаще всего имеют в виду их эффективные (действующие) значения U, I, равные 0,7 (точнее, 1 /√2) от амплитудных Um, lm, т. е. U = 0,7Um, I = 0,7lm. Расчеты можно производить как с амплитудными, так и с эффективными значениями, результат будет получаться, разумеется, в тех же значениях. Надо еще раз заметить, что это верно только для чисто синусоидального сигнала. Сигналы другой формы имеют совершенно другие соотношения между амплитудными, средними и эффективными значениями. Для сигнала прямоугольной формы, например, амплитудные значения напряжения и тока равны эффективным, а для сигнала в виде коротких импульсов амплитуда может в десятки раз превосходить эффективное значение. Среднее же за период значение чисто переменного тока (без постоянной составляющей) равно нулю. Соотношение между амплитудным и эффективным значением несинусоидального сигнала изменяется при прохождении им цепей с реактивными элементами, что надо постоянно иметь в виду. Обращайте внимание и на то, какие значения показывают используемые вами измерительные приборы. Простой пример измерения сетевого напряжения: вольтметр магнитоэлектрической системы, реагирующий на среднее значение, покажет 0, вольтметр электромагнитной системы - эффективное значение 220 В, вольтметр с пиковым детектором - более 300 В. Но вернемся к расчетам на переменном токе. Если в цепи имеются только активные сопротивления, расчет производится точно так же, как и в цепях постоянного тока с помощью закона Ома и правил Кирхгофа. Иное дело, если в цепи установлены катушки индуктивности и конденсаторы. Обычная алгебра здесь уже не пригодна, и необходимо пользоваться комплексными числами. Полное сопротивление катушки индуктивности складывается из активного сопротивления провода и индуктивного сопротивления обмотки. Последнее имеет характерные особенности: во-первых, оно растет пропорционально частоте переменного тока (на постоянном токе оно равно нулю), во-вторых, напряжение, которое выделяется на нем, опережает ток на 90° по фазе. Отношение индуктивного сопротивления катушки к активному называется добротностью и составляет обычно от нескольких единиц для низкочастотных катушек до нескольких сотен для высокочастотных. Конденсаторы, как правило, имеют весьма высокую добротность, и их емкостное сопротивление обратно пропорционально частоте. Напряжение на конденсаторе отстает на 90° по фазе от тока. Индуктивное и емкостное сопротивления называются реактивными. В отличие от активных, на них не рассеивается мощность - она лишь может накапливаться в катушке и конденсаторе и отдаваться обратно в цепь. По этой причине реактивные сопротивления являются не действительными, а мнимыми величинами и при расчетах перед их обозначением ставится знак j = √-1. Далее все алгебраические операции производятся обычным образом с учетом правил: 1/j = -j, j2 = -1. Полное сопротивление цепи Z = r + jX содержит действительную часть - активное сопротивление r и мнимую часть - реактивное сопротивление X, причем XL = jωL, XC - 1/jωC = - j/ωC. Индуктивное XL и емкостное XC сопротивления имеют разные знаки, что и указывает на опережение или отставание напряжения на данном сопротивлении относительно тока. В ряде случаев полезно знать абсолютное значение, или модуль полного сопротивления IZI=√r2+X2. В качестве примера найдем полное сопротивление цепи, содержащей резистор, катушку индуктивности и конденсатор (рис. 13): Z=r+jωL+1/jωC = r+j(ωL-1/jωC) = r+jX.
Мы видим, что активное сопротивление r от частоты не зависит, в то время как реактивное X зависит, и весьма значительно. На рис. 14 приведены графики, показывающие, как изменяются с частотой индуктивное, емкостное и общее реактивное сопротивления цепи X. Последнее обращается в нуль на некоторой частоте ω0 - резонансной частоте.
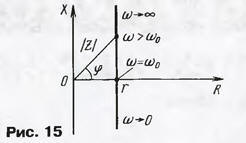
На резонансной частоте индуктивное сопротивление равно емкостному, а знаки у них разные, поэтому они и компенсируются. Легко найти:ω0L = 1/ω0С; ω02 = 1/LC. Отсюда получается широко известная формула Томсона для резонансной частоты колебательного контура, состоящего из катушки и конденсатора: f0 = 1/(2π√LC). Раз уж мы заговорили о контуре, то полезно упомянуть еще один важный параметр - добротность контура. Она равна отношению модуля р реактивного сопротивления катушки или конденсатора на резонансной частоте (где они равны) к активному сопротивлению r: Q = р/r. Если конденсатор имеет пренебрежимо малые потери, что обычно выполняется, то добротность контура равна добротности катушки. Реактивное сопротивление на резонансной частоте можно узнать, не вычисляя самой резонансной частоты: р = √L/C. Добротность получается максимальной (конструктивной) и может достигать нескольких сотен, если сопротивление r является лишь сопротивлением провода катушки и никаких дополнительных сопротивлений в цепь не включено. Полное сопротивление цепи, показанной на рис. 13, можно изобразить точкой в системе координат, где по горизонтальной оси отложены активные сопротивления, а по вертикальной - реактивные (рис. 15).
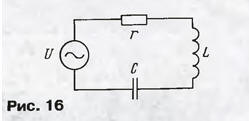
Именно так обычно и изображают числа на комплексной плоскости. При низкой частоте в цепи преобладает емкостное (отрицательное реактивное) сопротивление и точка расположится значительно ниже горизонтальной оси (случай ω→0). На резонансной частоте Z = r, а X = 0. На частотах, выше резонансной, точка расположится выше горизонтальной оси (случай ω-∞). Геометрическое место всех точек для разных частот образует вертикальную прямую линию, и на любой частоте очень легко графически найти модуль полного сопротивления, как показано для некоторой частоты ω>ω0. Пусть теперь выводы цепи (см. рис. 13) присоединены к источнику переменного напряжения U (генератору стандартных сигналов с пренебрежимо малым внутренним сопротивлением), частоту которого можно изменять (рис. 16).
Ток в цепи по-прежнему находится с помощью закона Ома: I = U/Z. Разумеется, ток будет переменным, с той же самой частотой, что и у источника, и если U - это эффективное значение напряжения, то и I будет эффективным значением тока. Но ведь Z - комплексная величина! Значение тока тоже получится комплексным, что означает сдвиг тока по фазе относительно приложенного напряжения. Поступим проще: поделим напряжение на модуль полного сопротивления и получим модуль тока: |l| =U/|Z|. Нужно узнать фазу тока? Она у нас уже есть - это угол <р на графике рис. 15. Действительно, для низких частот ток через емкостное сопротивление опережает напряжение (φ отрицательно), на резонансной частоте φ = 0, на высоких частотах ток через индуктивное сопротивление отстает от напряжения (φ положительно). Теперь нам легко построить резонансные кривые - значения амплитуды (рис. 17,а) и фазы тока (рис. 17,б) в последовательном резонансном контуре в зависимости от частоты.
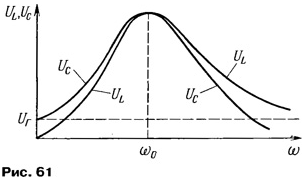
Вопрос для самопроверки. Постройте (хотя бы приблизительно) графики зависимости напряжения на катушке и на конденсаторе в зависимости от частоты в этом эксперименте (для контура, показанного на рис. 16). Попробуйте также ответить на вопрос, во сколько раз это напряжение больше (или меньше) напряжения генератора при добротности контура Q - 100? Ответ нужен с точностью не выше нескольких процентов. Ответ. Контур состоит из последовательно включенных генератора, активного сопротивления, индуктивности и емкости. Для того чтобы узнать напряжение на катушке и на конденсаторе, надо ток в цепи помножить на сопротивление этих элементов. На резонансной частоте реактивные сопротивления катушки и конденсатора равны, но противоположны по знаку, поэтому компенсируются. Ток в цепи равен U/r. Напряжения на катушке UL и конденсаторе Uc равны друг другу, противофазны и составляют Up/r = UQ. Таким образом, на резонансной частоте они в Q = 100 раз больше напряжения генератора. При понижении частоты ток в цепи уменьшается, реактивное сопротивление катушки также уменьшается, поэтому напряжение на катушке UL стремится к нулю. Емкостное же сопротивление растет, поэтому напряжение на конденсаторе Uc уменьшается не так быстро и стремится не к нулю, а к напряжению генератора U. Это легко усмотреть из схемы рис. 16 - на самых низких частотах емкостное сопротивление намного больше индуктивного и активного, поэтому практически все напряжение генератора оказывается приложенным к конденсатору. При повышении частоты (выше резонансной) ток в цепи и емкостное сопротивление уменьшаются и Uс стремится к нулю. Напряжение же на катушке UL из-за увеличения ее реактивного сопротивления стремится не к нулю, а к напряжению генератора. Графики частотной зависимости напряжений UL и UC похожи на график тока (рис. 17), но боковые ветви графиков приподняты, в первом случае - справа (в области высоких частот), во втором случае - слева (в области низких частот), как показано на рис. 61.
Автор: В.Поляков, г.Москва
Искусственная кожа для эмуляции прикосновений
15.04.2024 Кошачий унитаз Petgugu Global
15.04.2024 Привлекательность заботливых мужчин
14.04.2024
▪ Юпитер лишил Солнечную систему планеты
▪ раздел сайта Параметры радиодеталей. Подборка статей ▪ статья Лейбниц Готфрид. Биография ученого ▪ статья Где еще есть кофеин кроме чая и кофе? Подробный ответ ▪ статья Оператор линии розлива молока и молочной продукции в бутылки. Должностная инструкция ▪ статья Мигающая лампа. Энциклопедия радиоэлектроники и электротехники
Главная страница | Библиотека | Статьи | Карта сайта | Отзывы о сайте
www.diagram.com.ua |
Смотрите другие статьи раздела 
Последние новости науки и техники, новинки электроники:
All languages of this page