Бесплатная техническая библиотека

Парадокс с числами Фибоначчи. Секрет фокуса

Справочник / Эффектные фокусы и их разгадки

 Комментарии к статье

Описание фокуса:

Длины сторон четырех частей, составляющих фигуры (рис. 1 и 2), являются членами ряда Фибоначчи, т. е. ряда чисел, начинающегося с двух единиц: 1, 1, каждое из которых, начиная с третьего, есть сумма двух предшествующих. Наш ряд имеет вид 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

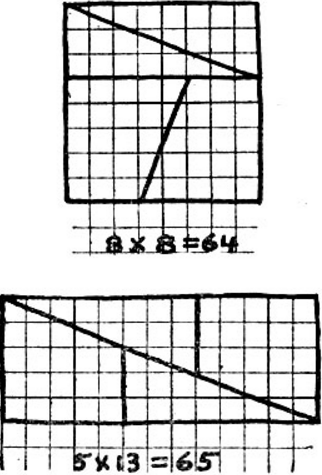
Рис.1

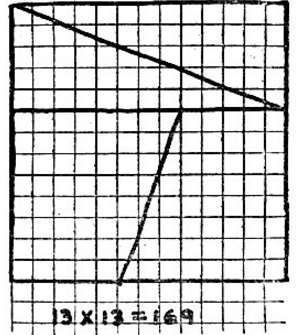
Рис. 2

Расположение частей, на которые был разрезан квадрат, в виде прямоугольника иллюстрирует одно из свойств ряда Фибоначчи, а именно следующее: при возведении в квадрат любого члена этого ряда получается произведение двух соседних членов ряда плюс или минус единица. В нашем примере сторона квадрата равна 8, а площадь равна 64. Восьмерка в ряду Фибоначчи расположена между 5 и 13. Так как числа 5 и 13 становятся длинами сторон прямоугольника, то площадь его должна быть равной 65, что дает прирост площади в одну единицу.

Благодаря этому свойству ряда можно построить квадрат, стороной которого является любое число Фибоначчи, большее единицы, а затем разрезать: его в соответствии с двумя предшествующими числами этого ряда.

Если, например, взять квадрат в 13 х 13 единиц, то три его стороны следует разделить на отрезки длиной в 5 и 8 единиц, а затем разрезать, как показано на рис. 2. Площадь этого квадрата равна 169 квадратным единицам. Стороны прямоугольника, образованного частями квадратов, будут 21 и 8, что дает площадь в 168 квадратных единиц. Здесь благодаря перекрыванию частей вдоль диагонали одна квадратная единица не прибавляется, а теряется.

Если взять квадрат со стороной 5, то тоже произойдет потеря одной квадратной единицы. Можно сформулировать и общее правило: приняв за сторону квадрата какое-нибудь число из "первой" подпоследовательности расположенных через одно чисел Фибоначчи (3, 8, ...) и составив из частей этого квадрата прямоугольник, мы получим вдоль его диагонали про свет и как следствие кажущийся прирост площади на одну единицу. Взяв же за сторону квадрата какое-нибудь число из "второй" подпоследовательности (2, 5, 13, ...), мы получим вдоль диагонали прямоугольника перекрывание площадей и потерю одной квадратной единицы площади.

Чем дальше мы продвигаемся по ряду чисел Фибоначчи, тем менее заметными становятся перекрывания или просветы. И наоборот, чем ниже мы спускаемся по ряду, тем они становятся более существенными. Можно построить парадокс даже на квадрате со стороной в две единицы. Но тогда в прямоугольнике 3х1 получается столь очевидное перекрывание, что эффект парадокса полностью теряется.

Используя для парадокса другие ряды Фибоначчи, можно получить: бесчисленное множество вариантов. Так, например, квадраты, основанные на ряде 2, 4, 6, 10, 16, 26 и т.д., приводят к потерям или приростам площади в 4 квадратные единицы. Величину этих потерь или приростов можно узнать, вычисляя для данного ряда разности между квадратом любого его члена и произведением двух его соседних членов слева и справа. Ряд 3,4,7, И, 18,29 и т.д. дает прирост или потерю в пять квадратных единиц.

Т. де Мулидар привел рисунок квадрата, основанного на ряде 1, 4, 5, 9, 14 и т. д. Сторона этого квадрата взята равной 9, и после преобразования его в прямоугольник теряется 11 квадратных единиц. Ряд 2, 5, 7, 12, 19,... также дает потерю или прирост в 11 квадратных единиц. В обоих случаях перекрывания (или просветы) вдоль диагонали оказываются настолько большими, что их сразу можно заметить.

Обозначив какие-нибудь три последовательных числа Фибоначчи через А, В и С, а через X - потерю или прирост площади, мы получим следующие две формулы:

А+В=С

В2=АС±Х.

Если подставить вместо X желаемый прирост или потерю, а вместо В число, которое принято за длину стороны квадрата, то можно построить квадратное уравнение, из которого найдутся два других числа Фибоначчи, хотя это, конечно, не обязательно будут рациональные числа. Оказывается, например, что, деля квадрат на фигуры с рациональными длинами сторон, нельзя получить прирост или потерю в две или три квадратные единицы. С помощью иррациональных чисел это, конечно, можно достигнуть. Так, ряд Фибоначчи √2, 2√2, 3√2, 5√ ... дает прирост или потерю в две квадратные единицы, а ряд √3, 2√3, 3√3, 5√3, ... приводит к приросту или потере в три квадратные единицы.

Автор: М.Гарднер

 Рекомендуем интересные статьи раздела Эффектные фокусы и их разгадки:

▪ Остающиеся деньги

▪ Одна против восьми

▪ Палочка наколдовывает конфеты

Смотрите другие статьи раздела Эффектные фокусы и их разгадки.

Читайте и пишите полезные комментарии к этой статье.

<< Назад

Последние новости науки и техники, новинки электроники:

Оптимальная продолжительность сна 12.11.2025

Сон играет ключевую роль в поддержании здоровья, когнитивных функций и общего самочувствия. Несмотря на широко распространенный стереотип о восьмичасовом сне, последние исследования показывают, что оптимальная продолжительность сна для большинства здоровых взрослых ближе к семи часам. Эволюционный биолог из Гарварда, Дэниел Э. Либерман, утверждает, что традиционная норма восьми часов сна - это скорее культурное наследие индустриальной эпохи, чем биологическая необходимость. По его словам, полевые исследования, проведенные в сообществах, не использующих электричество, показывают, что средняя продолжительность сна составляет 6-7 часов, что значительно отличается от общепринятого стандарта. Современные эпидемиологические данные подтверждают этот взгляд. Исследования выявили так называемую "U-образную кривую" зависимости между продолжительностью сна и рисками для здоровья. Минимальные показатели заболеваемости и смертности наблюдаются именно у людей, спящих около семи часов в сутки. ...>>

Дефицит кислорода усиливает выброс закиси азота 12.11.2025

Парниковые газы играют ключевую роль в изменении климата, а закись азота (N2O) - один из наиболее опасных среди них. Этот газ не только втрое сильнее углекислого газа в удержании тепла, но и разрушает озоновый слой. Недавнее исследование американских ученых показало, что микробы в зонах с низким содержанием кислорода активно производят N2O, усиливая глобальные климатические риски. Команда из Университета Пенсильвании изучала прибрежные воды у Сан-Диего и провела наблюдения на глубинах от 40 до 120 метров в Восточной тропической северной части Тихого океана - одной из крупнейших зон дефицита кислорода. Исследователи сосредоточились на том, как морские микроорганизмы превращают нитраты в закись азота. В ходе работы выяснилось, что существует два пути образования N2O. Один путь начинается с нитрата, другой - с нитрита. На первый взгляд более короткий путь должен быть эффективнее, однако микробы, использующие нитрат, продуцируют больше газа, поскольку этот "сырьевой" источник более д ...>>

Омега-3 помогают молодым кораллам выживать 11.11.2025

Сохранение коралловых рифов становится все более актуальной задачей в условиях глобального изменения климата. Молодые кораллы особенно уязвимы на ранних стадиях развития, когда стрессовые условия и нехватка питательных веществ могут привести к высокой смертности. Недавнее исследование ученых из Технологического университета Сиднея показывает, что специальные пищевые добавки способны существенно повысить выживаемость личинок кораллов. В ходе работы исследователи разработали особый состав "детского питания" для коралловых личинок. В него вошли масла, богатые омега-3 жирными кислотами, а также важные стерины, необходимые для формирования клеточных мембран. Личинки, получавшие эти добавки, развивались быстрее, становились крепче и демонстрировали более высокую устойчивость к стрессовым факторам. Особое внимание ученые уделили липидам. Анализ показал, что личинки активно усваивают эти вещества, что напрямую влияет на их жизнеспособность. Стерины, содержащиеся в корме, повышают устойчи ...>>

Случайная новость из Архива Создан квантовый кристалл 18.11.2012 И драгоценный алмаз, и дешевый графит состоят из одинаковых атомов углерода. Крошечным, но очень важным отличием этих материалов является геометрическая конфигурация их блоков. Один и тот же материал не может быть одновременно и алмазом, и графитом. Однако в квантовой физике такого ограничения нет - это продемонстрировала команда физиков во главе с профессором Иммануилом Блохом из Института квантовой оптики Макса Планка и Людвигом Максимиллианом из Мюнхенского Университета. Эксперименты проводились с ультраохлажденным квантовым газом. Под воздействием лазерного луча отдельные атомы можно упорядочить в правильные геометрические структуры. Но в отличие от классических кристаллов все возможные конфигурации квантового кристалла будут существовать одновременно. Это наблюдение было сделано после перехода частиц в т.н. ридберговское состояние, при котором они сильно возбуждаются энергией светового пучка. "Наш эксперимент демонстрирует потенциал Ридберговских газов для создания новых состояний материи. Тем самым мы закладываем основу для квантового моделирования, например, квантовых магнитов", - говорит Иммануил Блох. Эксперимент начался с охлаждения ансамбля из нескольких сотен атомов рубидия до температур, близких к абсолютному нулю, и поимки атомов в световую ловушку. Затем на атомное облако накладывалась периодическая световая решетка - т.н. оптическая решетка, обеспечивающая практически равномерное заполнение в центральной части атомной ловушки. Далее при помощи лазера атомы приводились в ридберговское состояние, в котором внешняя электронная оболочка находится на огромном расстоянии от ядра. В результате область воздействия этих атомов выросла примерно в 10 000 раз до просто огромного размера - нескольких микрометров, порядка 1/10 человеческого волоса. Теперь эти атомы начали взаимодействовать через т.н. силы Ван-дер-Ваальса. Взаимное отталкивание этих атомов приводит к тому, что они располагаются на расстоянии в несколько микрометров друг от друга. Возникает пространственная корреляция между атомами, что, в зависимости от количества возбужденных атомов, приводит к разным геометриям кристаллической решетки. Если точнее, все возможные кристаллические решетки существуют там одновременно. Это новое состояние вещества является очень хрупким, оно существует, только пока включен лазерный луч и атомы возбуждены. Делая "мгновенные снимки" таких конфигураций специальной техникой с высочайшим разрешением, ученые выявили различные геометрии этого кристалла. Типичные конфигурации - это три атома в равностороннем треугольнике, четыре или пять образуют квадраты и правильные пятиугольники. Эксперименты хорошо согласуются с предсказаниями численного моделирования.

Другие интересные новости:

▪ Конец видеомагнитофонов от PANASONIC

▪ Кофе - защита от инсульта

▪ Технология формирования физических клавиш на сенсорных дисплеях

▪ Интеллект и социальные контакты

▪ Чип TDA15600 для управления ЖК экраном телевизора

Лента новостей науки и техники, новинок электроники

Интересные материалы Бесплатной технической библиотеки:

▪ раздел сайта Индикаторы, датчики, детекторы. Подборка статей

▪ статья Суперкомпьютер. История изобретения и производства

▪ статья Где находятся мышцы, которые позволяют шевелить ушами? Подробный ответ

▪ статья Пользователь (оператор) компьютера (ПЭВМ). Типовая инструкция по охране труда

▪ статья Индикаторы к спаренному телефону. Энциклопедия радиоэлектроники и электротехники

▪ статья В геометрический центр. Секрет фокуса

Оставьте свой комментарий к этой статье:

www.diagram.com.ua
2000-2025